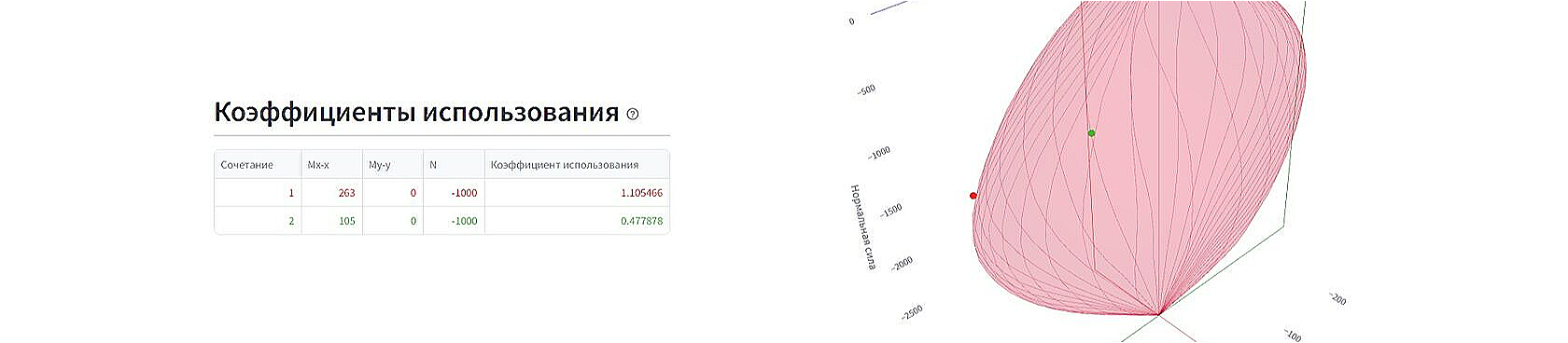
Коэффициент использования
Чтение: 3 мин.
Определение коэффициента использования
Для того, чтобы оценить, насколько действующие усилия близки к предельным, вводится понятие коэффициента использования:
\[К_{исп} = \frac {F} {F_u}\]
где
F — действующие усилия;
Fu — предельные усилия.
F — действующие усилия;
Fu — предельные усилия.
Критерий по прочности сечения
Значения коэффициента использования:
Значения коэффициента использования:
- меньшие или равные 1 означают, что критерий прочности соблюдается;
- больше 1 — критерий не соблюдается.
В случае, когда в сечении совместного действуют продольная сила и изгибающие моменты, возникает вопрос “как оценивать значение критерия?”, ведь компонент усилий не одна, а несколько.
Удобнее всего оценивать “длины” (или, говоря математическим языком, нормы) усилий.
Такая “длина” находится как корень из суммы квадратов длин отрезков, соединяющих начало координат с точкой, обозначающей действующие усилия.
Например:
Такая “длина” находится как корень из суммы квадратов длин отрезков, соединяющих начало координат с точкой, обозначающей действующие усилия.
Например:
\[F = \sqrt {M^2 + N^2}\]
Здесь M и N принимаются безразмерными величинами, численно равными изгибающему моменту и продольной силе.
С геометрической точки зрения это длина гипотенузы прямоугольного треугольника со сторонами |M| и |N|.
С геометрической точки зрения это длина гипотенузы прямоугольного треугольника со сторонами |M| и |N|.
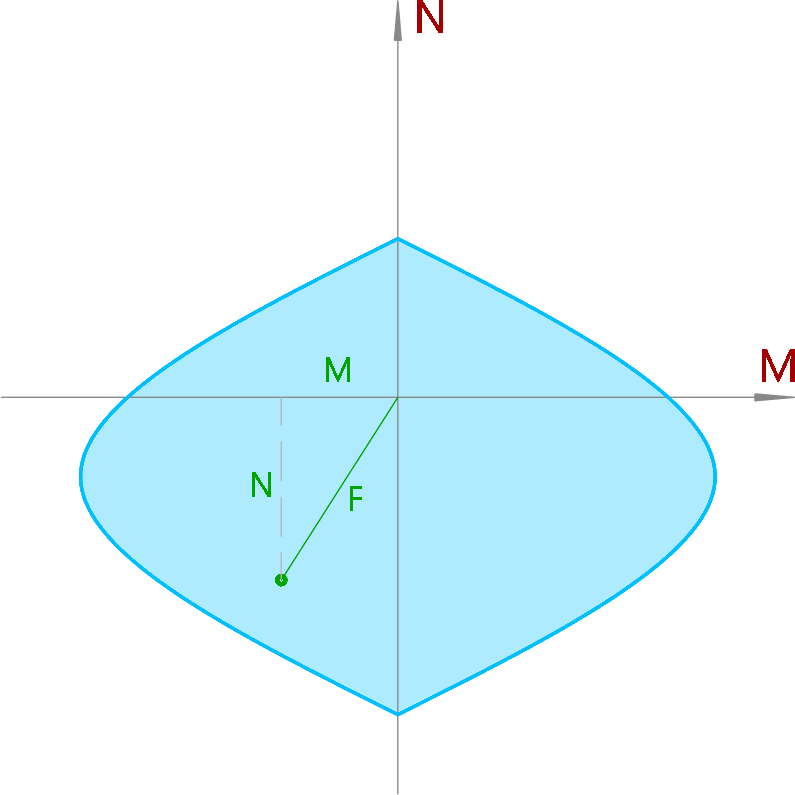
Для определения “длины” предельных усилий достаточно найти точку пересечения луча, который идёт из начала координат и проходит через точку действующих усилий, с поверхностью предельных усилий:
\[F_u = \sqrt { {M_u}^2 + {N_u}^2 }\]
Отношение этих двух величин даст чёткое и понятное значение коэффициента использования:
\[К_{исп} = \frac {F} {F_u} = \frac {\sqrt {M_{ }^2 + N_{ }^2}} {\sqrt { {M_u}^2 + {N_u}^2 }}\]
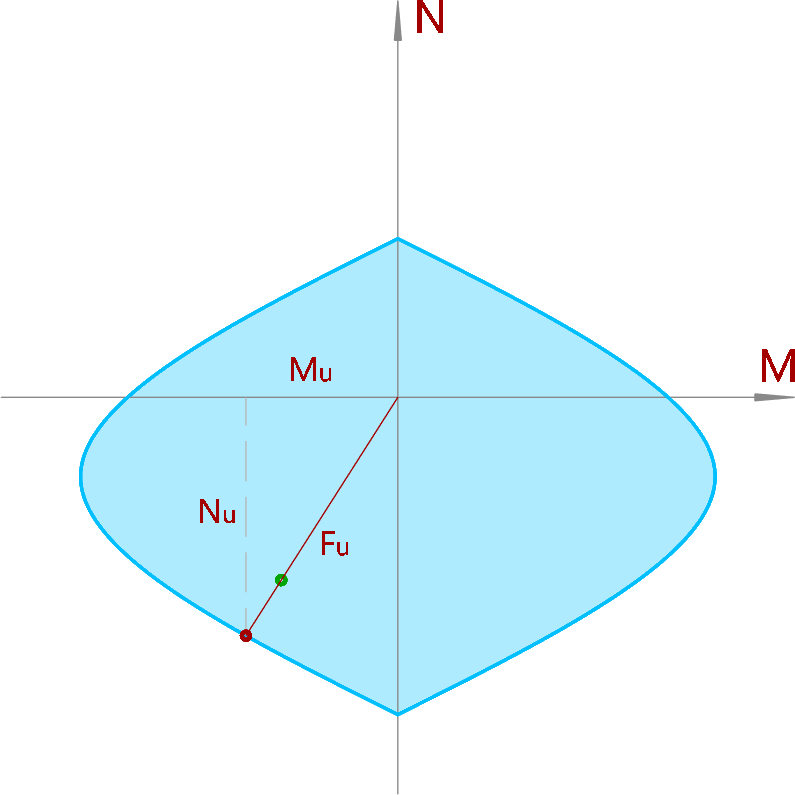
Вычисленный таким образом коэффициент использования покажет, во сколько раз нужно увеличить или уменьшить действующие усилия, чтобы они сравнялись с предельными.
Случай с моментами в двух направлениях
Если в сечении действуют моменты в обоих направлениях, то “длина” усилий находится аналогично:
Если в сечении действуют моменты в обоих направлениях, то “длина” усилий находится аналогично:
\[F = \sqrt {M_{x-x}^2 + M_{y-y}^2 + N^2}\]
\[F_{u} = \sqrt {M_{x-x,u}^2 + M_{y-y,u}^2 + N_{u}^2}\]
Здесь Mx-x, My-y и N принимаются безразмерными величинами, численно равными изгибающим моментам относительно осей X и Y и продольной силе соответственно.
С геометрической точки зрения это длина диагонали параллелепипеда со сторонами |Mx-x|, |My-y| и |N|.
С геометрической точки зрения это длина диагонали параллелепипеда со сторонами |Mx-x|, |My-y| и |N|.
