Расчет трещин
Чтение: 5 мин.
Расчет по образованию нормальных трещин
Для оценки возможности образования трещин в нормальном сечении используется поверхность предельных усилий в координатах Mx−x−My−y−N, как и для проверки по прочности.
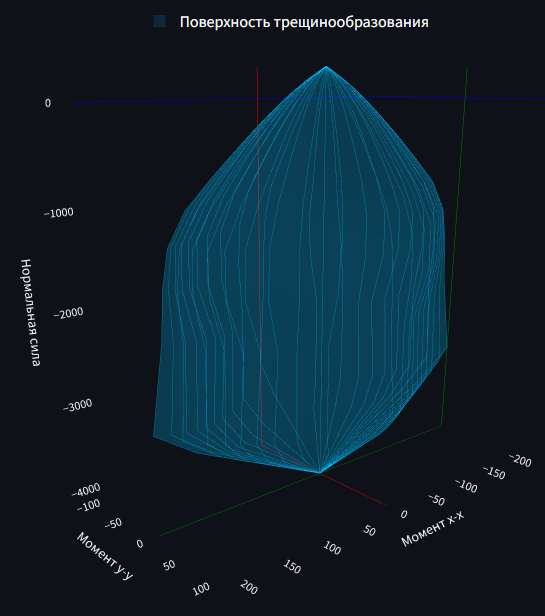
Поверхность трещинообразования
Для её построения используются следующие критерии:
- предельная деформация при растяжении εtu = εbt2;
- предельная деформация при сжатии εcu = εb2,
εbt2 и εb2 — предельные деформации бетона при растяжении и сжатии соответственно.
Принцип проверки
Если точка с усилиями лежит внутри поверхности, то трещины не образуются.
Если точка лежит за пределами поверхности, то трещины могут образовываться. В этом случае производится расчёт ширины раскрытия трещин.
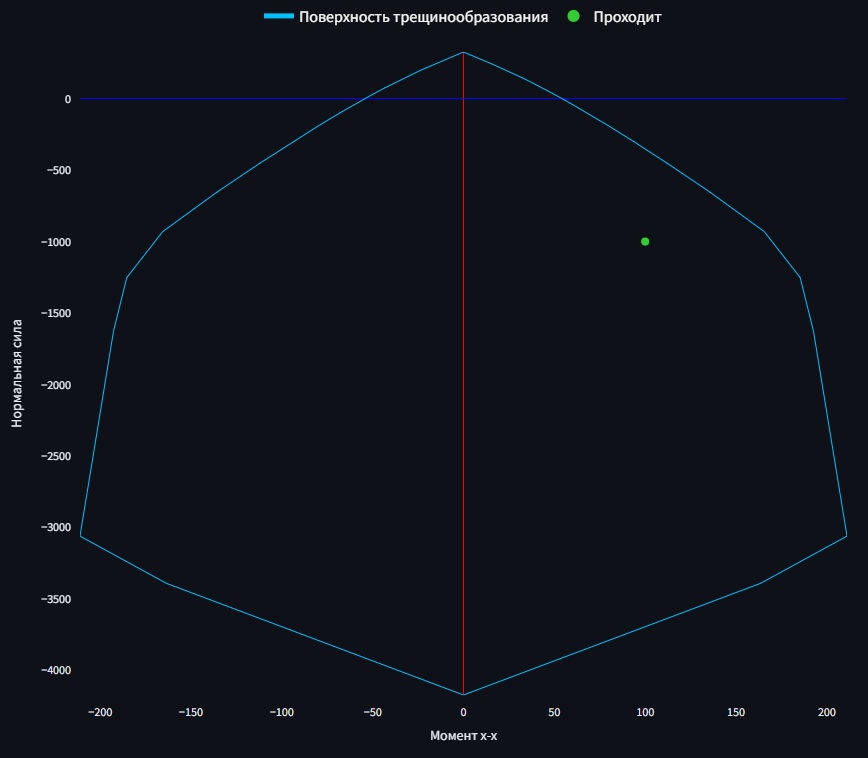
Точка с усилиями лежит внутри поверхности — трещины не образуются
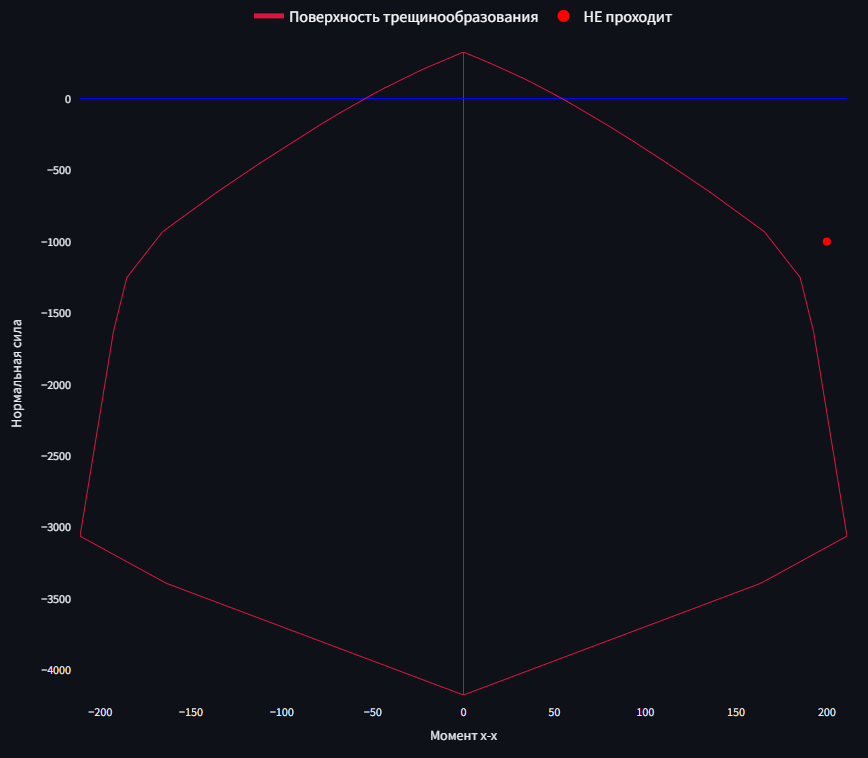
Точка с усилиями лежит снаружи поверхности — трещины образуются
Выход точки за пределы поверхности в той области, где сечение полностью сжато, говорит не об образовании трещин, а об исчерпании несущей способности сечения при сжатии.
Такая ситуация не должна возникать, когда коэффициент использования по прочности нормальных сечений меньше 1,0, то есть прочность сечения обеспечена.
Для расчётов по второй группе предельных состояний используются более высокие значения расчётного сопротивления материалов, а усилия напротив принимаются с более низкими коэффициентами надёжности. Поэтому описанная выше ситуация крайне маловероятна при условии достаточной несущей способности сечения.
Такая ситуация не должна возникать, когда коэффициент использования по прочности нормальных сечений меньше 1,0, то есть прочность сечения обеспечена.
Для расчётов по второй группе предельных состояний используются более высокие значения расчётного сопротивления материалов, а усилия напротив принимаются с более низкими коэффициентами надёжности. Поэтому описанная выше ситуация крайне маловероятна при условии достаточной несущей способности сечения.
Коэффициент использования по образованию трещин
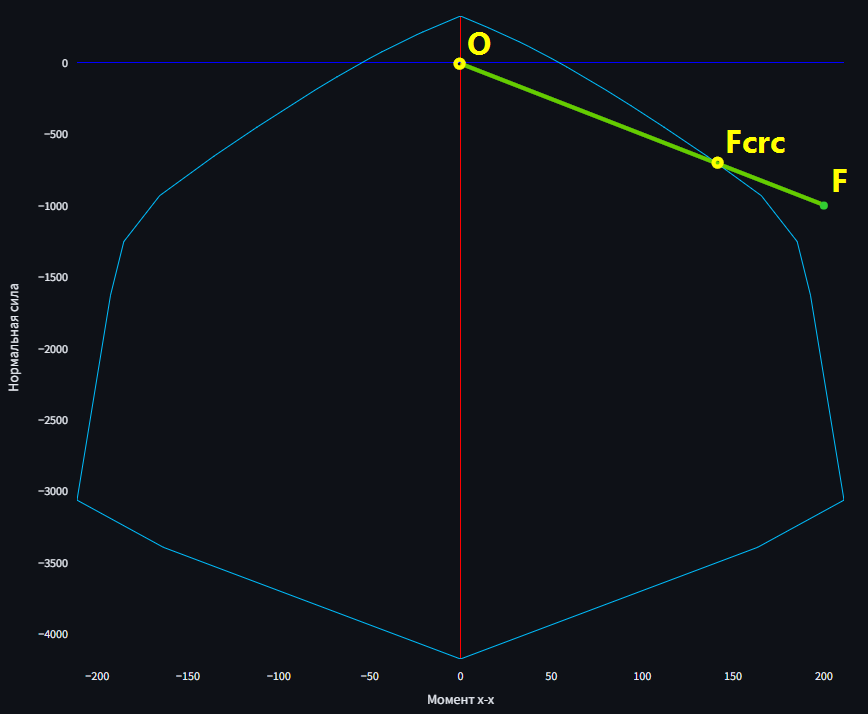
К расчёту коэффициента использования по образованию трещин
Коэффициент использования по образованию нормальных трещин вычисляется также, как и для расчётов по прочности.
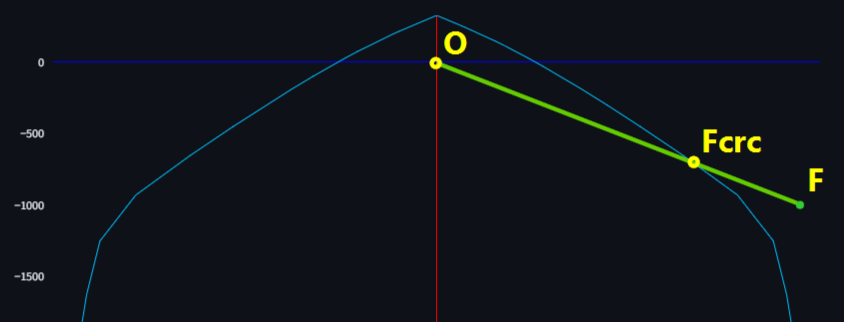
- Вычисляется длина отрезка, проведённого из начала координат O до точки, обозначающей действующие усилия F.
- Определяется точка пересечения луча, проведённого из O через F, с поверхностью трещинообразования. Обозначим эту точку Fcrc.
- Коэффициент использования вычисляется как отношение длин отрезков OF и OFcrc, то есть:
\[К_{исп} = \frac {OF} {OF_{crc}}\]
или
\[К_{исп} = \frac {|\overline F|} {|\overline F_{crc}|}\]
Если коэффициент использования оказывается больше 1,0 и трещины допускаются, то производится вычисление ширины их раскрытия.
Расчет ширины раскрытия нормальных трещин
Ширина раскрытия трещин, нормальных к продольной оси элемента, зависит от деформаций арматуры εs, деформаций растянутого бетона εbt и расстояния между трещинами Ls [2].
Помимо этого она зависит от длительности приложенной нагрузки, вида арматуры и типа напряжённо-деформированного состояния. Влияние этих факторов обычно учитывается эмпирическими коэффициентами.
В разных нормах проектирования используются различные формулы для вычисления ширины раскрытия трещин.
Ширина раскрытия трещин, нормальных к продольной оси элемента, зависит от деформаций арматуры εs, деформаций растянутого бетона εbt и расстояния между трещинами Ls [2].
Помимо этого она зависит от длительности приложенной нагрузки, вида арматуры и типа напряжённо-деформированного состояния. Влияние этих факторов обычно учитывается эмпирическими коэффициентами.
В разных нормах проектирования используются различные формулы для вычисления ширины раскрытия трещин.
Расчет ширины раскрытия трещин, нормальных к продольной оси элемента, приведен в п.8.2.15 СП 63.13330.2018
Ширина раскрытия нормальных трещин вычисляется по формуле [1]:
\[a_{crc} = \varphi_1 \cdot \varphi_2 \cdot \varphi_3 \cdot \psi_s \frac {\sigma_s} {E_s} L_s \space\space\space\space\space(1)\]
где
φ1 — коэффициент, учитывающий продолжительность действия нагрузки; при продолжительном действии нагрузки φ1 = 1,4, при непродолжительном действии φ1 = 1,0.
φ2 — коэффициент, учитывающий профиль продольной арматуры; для арматуры периодического профиля и канатов φ2 = 0,5, для гладкой арматуры φ2 = 0,8.
φ3 — коэффициент, учитывающий характер нагружения; для изгибаемых и внецентренно сжатых элементов φ3 = 1,0, для растянутых элементов φ3 = 1,2.
ψs — коэффициент, учитывающий работу бетона между трещинами;
σs — напряжения в растянутой арматуре;
Es — модуль упругости арматурной стали;
Ls — расстояние между трещинами.
В СП 63.13330 не приводится критерия, по которому сечение считается растянутым. Поэтому для исключения ситуации, в которой появление сколь угодно малой растягивающей продольной силы приводило бы к изменению значения ширины раскрытия трещин на 20% из-за изменения значения коэффициента φ3, введено следующее правило:
φ1 — коэффициент, учитывающий продолжительность действия нагрузки; при продолжительном действии нагрузки φ1 = 1,4, при непродолжительном действии φ1 = 1,0.
φ2 — коэффициент, учитывающий профиль продольной арматуры; для арматуры периодического профиля и канатов φ2 = 0,5, для гладкой арматуры φ2 = 0,8.
φ3 — коэффициент, учитывающий характер нагружения; для изгибаемых и внецентренно сжатых элементов φ3 = 1,0, для растянутых элементов φ3 = 1,2.
ψs — коэффициент, учитывающий работу бетона между трещинами;
σs — напряжения в растянутой арматуре;
Es — модуль упругости арматурной стали;
Ls — расстояние между трещинами.
В СП 63.13330 не приводится критерия, по которому сечение считается растянутым. Поэтому для исключения ситуации, в которой появление сколь угодно малой растягивающей продольной силы приводило бы к изменению значения ширины раскрытия трещин на 20% из-за изменения значения коэффициента φ3, введено следующее правило:
- при N ≥ 0,1⋅Nu принимается φ3 = 1,2;
- при N ≤ 0 принимается φ3 = 1,0;
- при 0 < N < 0,1 ⋅ Nu принимается:
\[\varphi_{3} =1,0 + 0,2 \cdot \frac {N} {0,1 N_{max}}\]
где
Nu — максимальная растягивающая продольная сила, которую может воспринимать сечение.
Коэффициент ψs вычисляется по формуле:
Nu — максимальная растягивающая продольная сила, которую может воспринимать сечение.
Коэффициент ψs вычисляется по формуле:
\[\psi_s = 1 - 0.8 \cdot \frac {\sigma_{s,crc}} {\sigma_{s}}\]
и принимается в пределах от 0,2 до 1,0 [3].
Ширина раскрытия трещин вычисляется в предположении упругой работы арматуры, то есть деформации и напряжения в арматуре связаны через модуль упругости арматурной стали:
Ширина раскрытия трещин вычисляется в предположении упругой работы арматуры, то есть деформации и напряжения в арматуре связаны через модуль упругости арматурной стали:
\[\varepsilon_{s} = \frac {\sigma_s} {E_s}\]
Преобразуем формулу (1) к виду:
\[a_{crc} = \varphi_{1} \cdot \varphi_{2} \cdot \varphi_{3} \cdot (1 - 0.8 \cdot \frac {\sigma_{s,crc}} {\sigma_{s}}) \frac {\sigma_{s}} {E_{s}} L_{s} =\]
\[= \varphi_{1} \cdot \varphi_{2} \cdot \varphi_{3} \cdot (\frac {\sigma_{s}} {E_{s}} - 0.8 \cdot \frac {\sigma_{s,crc}} {E_{s}}) L_{s} =\]
\[= \varphi_{1} \cdot \varphi_{2} \cdot \varphi_{3} \cdot (\varepsilon_{s} - 0.8 \cdot \varepsilon_{s,crc}) L_{s} \]
где
εs,crc — деформация в арматурном стержне, для которого определяется ширина раскрытия трещин, в сечении с трещиной сразу после образования трещин, то есть при действии усилий трещинообразования Fcrc.
Усилия трещинообразования Fcrc определяются в точке пересечения отрезка OF с поверхностью трещинообразования, как было описано выше.
εs,crc — деформация в арматурном стержне, для которого определяется ширина раскрытия трещин, в сечении с трещиной сразу после образования трещин, то есть при действии усилий трещинообразования Fcrc.
Усилия трещинообразования Fcrc определяются в точке пересечения отрезка OF с поверхностью трещинообразования, как было описано выше.

Определение усилий Fcrc
Расстояние между трещинами вычисляется по формуле:
\[L_{s} = \frac {1} {2} \frac {A_{bt}} {A_{s}} d_{s} \space \space \space \space \space (2)\]
где
Abt — площадь сечения растянутого бетона в сечении БЕЗ трещины при действии усилий трещинообразования Fcrc;
As — площадь сечения растянутой арматуры в сечении С трещиной при действии усилий F;
ds — диаметр растянутой арматуры.
СП 63.13330 приводит указания по определению Abt только для случая плоского изгиба и центрального сжатия. В этом случае Abt принимается:
a — расстояние от наиболее растянутой грани сечения до центра тяжести растянутой арматуры;
h — полная высота сечения.
Указанные пределы обусловлены включением в работу бетона, окружающего растянутую арматуру.
Для случая, когда изгибающие моменты действуют в двух направлениях, такие ограничения не приводятся. Тем не менее, чтобы соблюдать требования СП 63.13330 в части изгиба в одном направлении, площадь сечения растянутого бетона Abt принимается не более половины полной площади сечения.
В качестве диаметра растянутой арматуры ds принимается наибольший диаметр среди всех растянутых стержней (в запас).
Вычисленное по формуле (2) расстояние между трещинами корректируется с использованием следующих пределов:
Abt — площадь сечения растянутого бетона в сечении БЕЗ трещины при действии усилий трещинообразования Fcrc;
As — площадь сечения растянутой арматуры в сечении С трещиной при действии усилий F;
ds — диаметр растянутой арматуры.
СП 63.13330 приводит указания по определению Abt только для случая плоского изгиба и центрального сжатия. В этом случае Abt принимается:
- не менее 2a
- не более 0,5h
a — расстояние от наиболее растянутой грани сечения до центра тяжести растянутой арматуры;
h — полная высота сечения.
Указанные пределы обусловлены включением в работу бетона, окружающего растянутую арматуру.
Для случая, когда изгибающие моменты действуют в двух направлениях, такие ограничения не приводятся. Тем не менее, чтобы соблюдать требования СП 63.13330 в части изгиба в одном направлении, площадь сечения растянутого бетона Abt принимается не более половины полной площади сечения.
В качестве диаметра растянутой арматуры ds принимается наибольший диаметр среди всех растянутых стержней (в запас).
Вычисленное по формуле (2) расстояние между трещинами корректируется с использованием следующих пределов:
- 10ds ≤ Ls ≤ 40ds
- 10 см ≤ Ls ≤ 40 см
Порядок расчета ширины раскрытия трещин
1. Для арматурного стержня, который является самым растянутым при действии полных нагрузок, определяется ширина раскрытия трещин:
acrc = acrc1 + acrc2 − acrc3
3. Для арматурного стержня, который является самым растянутым при действии постоянных и длительных нагрузок (он может не совпадать со стержнем из п.1), определяется ширина раскрытия трещин от продолжительного действия постоянных и длительных нагрузок acrc, l. Это значение принимается в качестве ширины продолжительного раскрытия трещин.
1. Для арматурного стержня, который является самым растянутым при действии полных нагрузок, определяется ширина раскрытия трещин:
- от непродолжительного действия полных нагрузок acrc2.
- от продолжительного действия постоянных и длительных нагрузок acrc1.
- от непродолжительного действия постоянных и длительных нагрузок acrc3.
acrc = acrc1 + acrc2 − acrc3
3. Для арматурного стержня, который является самым растянутым при действии постоянных и длительных нагрузок (он может не совпадать со стержнем из п.1), определяется ширина раскрытия трещин от продолжительного действия постоянных и длительных нагрузок acrc, l. Это значение принимается в качестве ширины продолжительного раскрытия трещин.
Список используемых источников
[1] СП 63.13330.2018 “СНиП 52-01-2003 Бетонные и железобетонные конструкции. Основные положения” (с изменением N 2).
[2] Мурашев, В. И. Трещиноустойчивость, жесткость и прочность железобетона / В. И. Мурашев. – Москва, 1950. – 268 с.
[3] Кодыш, Э. Н. Расчет железобетонных конструкций из тяжелого бетона по прочности, трещиностойкости и деформациям / Э. Н. Кодыш, И. К. Никитин, Н. Н. Трекин. – Москва : Издательство Ассоциации строительных вузов (АСВ), 2011. – 352 с.
[1] СП 63.13330.2018 “СНиП 52-01-2003 Бетонные и железобетонные конструкции. Основные положения” (с изменением N 2).
[2] Мурашев, В. И. Трещиноустойчивость, жесткость и прочность железобетона / В. И. Мурашев. – Москва, 1950. – 268 с.
[3] Кодыш, Э. Н. Расчет железобетонных конструкций из тяжелого бетона по прочности, трещиностойкости и деформациям / Э. Н. Кодыш, И. К. Никитин, Н. Н. Трекин. – Москва : Издательство Ассоциации строительных вузов (АСВ), 2011. – 352 с.
